Funciones

FUNCIÓN LINEAL

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).



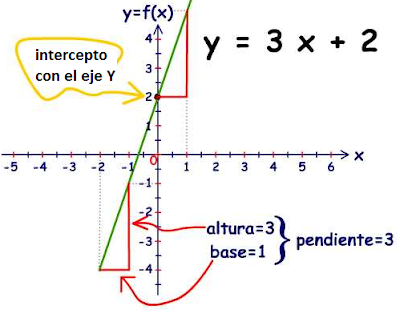
Esta es la gráfica de la función lineal y = 3x + 2


Vemos que m = 3 y b = 2 (de la forma y = mx + b)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)


Volvamos al ejemplo de las funciones lineales

f(x) = 3x+2 Si x es 3, entonces f (3) = 3*3+2 = 11

Si x es 4, entonces f (4) = 3*4+2 = 14

Si x es 5, entonces f (5) = 3*5+2 = 17

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 3 unidades. Si el valor de la pendiente es positivo la función es Creciente. Preste atención en que los valores de x y de f(x) NO SON PROPORCIONALES.

Lo que son proporcionales son los incrementos.

g(x) = -3x+7 Si x= 0, entonces g (0) = -3*(0) +7 = 0+7 = 7

Si x= 1, entonces g (1) = -3*(1) +7 = -3+7 = 4

Si x= 2, entonces g (2) = -3*(2) +7 = -6+7 = 1

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades. Si el valor de la pendiente es negativo la función es Decreciente.

h(x) = 4 Si x= 0 , entonces h(0) = 4

Si x= 98 entonces h(98) = 4

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje X.

Esta es la representación gráfica de los tres tipos de funciones descritas.

Ejercicios de Aplicación:

Representa las funciones

y = 2
y = -2
y = ¾
y = 0
x = 0
x = −5
y = x
y = 2x
y = 2x − 1
y = −2x − 1
y = ½x − 1
y = ½x − 1

             Función Exponencial

La función exponencial es del tipo:



Sea a un número real positivo.
La función que a cada número real x le hace
corresponder la potencia ax se llama función exponencial
de base a y exponente x.

Ejemplos

x	y = 2x
-3	1/8
-2	1/4
-1	1/2
0	1
1	2
2	4
3	8

Ejercicios de Aplicación:

y = (x − 1)² + 1

y = 3(x − 1)² + 1

y = 2(x + 1)² − 3

y = −3(x − 2)² − 5

y = x² − 7x −18

Función Cuadrática 

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

f(x) = ax² + bx + c
Representación gráfica de la parábola

Podemos construir una parábola a partir de estos puntos:
1. Vértice



Por el vértice pasa el eje de simetría de la parábola.

La ecuación del eje de simetría es:


2. Puntos de corte con el eje OX

En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:

ax² + bx + c = 0

Resolviendo la ecuación podemos obtener:

Dos puntos de corte: (x1, 0) y (x2, 0) si b² − 4ac > 0

Un punto de corte: (x1, 0) si b² − 4ac = 0

Ningún punto de corte si b² − 4ac < 0


3. Punto de corte con el eje OY

En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:

f(0) = a · 0² + b · 0 + c = c (0,c)

Representar la función f(x) = x² − 4x + 3.
1. Vértice

xv = − (−4) / 2 = 2 yv= 2² − 4· 2 + 3 = −1

V(2, −1)
2. Puntos de corte con el eje OX

x² − 4x + 3 = 0



(3, 0) (1, 0)
3. Punto de corte con el eje Y

(0, 3)

Orientación o concavidad

Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax2):

Si a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2 − 3x − 5





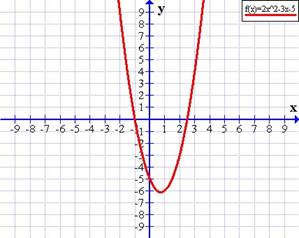
Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3


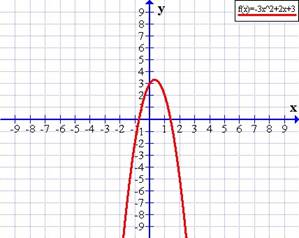
Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.

Ejercicios de Aplicación 

Representa gráficamente las funciones cuadráticas:

y = x² − 5x + 3

y = 2x² − 5x + 4

y = x² − 2x + 4

y = −x² − x + 3

y = −x² + 4x − 3

y = x² + 2x + 1

Función Logarítmica 

La función logarítmica en base a es la función inversa de la exponencial en base a.





Ejemplos

x
1/8	-3
1/4	-2
1/2	-1
1	0
2	1
4	2
8	3

x
1/8	3
1/4	2
1/2	1
1	0
2	−1
4	−2
8	−3

Propiedades de las funciones logarítmicas

Dominio:

Recorrido:

Es continua.

Los puntos (1, 0) y (a, 1) pertenecen a la gráfica.

Es inyectiva (ninguna imagen tiene más de un original).

Creciente si a>1.

Decreciente si a<1.

Las gráfica de la función logarítmica es simétrica (respecto a la bisectriz del 1er y 3er cuadrante) de la gráfica de la función exponencial, ya que son funciones reciprocas o inversas entre sí.

Definición de logaritmo



Siendo a la base, x el número e y el logaritmo.

Ejemplos


1.





2.





3.





4.





5.

De la definición de logaritmo podemos deducir:

No existe el logaritmo de un número con base negativa.



No existe el logaritmo de un número negativo.



No existe el logaritmo de cero.



El logaritmo de 1 es cero.



El logaritmo en base a de a es uno.



El logaritmo en base a de una potencia en base a es igual al exponente.



Propiedades de los logaritmos

1. El logaritmo de un producto es igual a la suma de los logaritmos de los factores.





2. El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.





3. El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.





4. El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz.





5. Cambio de base:

Logaritmos decimales
Son los que tienen base 10. Se representan por log (x).
Logaritmos neperianos
Son los que tienen base e. Se representan por ln (x) o L(x).

Ejercicios de Aplicación

1


2


3


4


5


6


7


8


9


10