Limites

De una función:

Sea f una función. Estamos interesados en el valor de la función f(x) cuando x se aproxima a un valor c, pero no es necesariamente igual a c. Esto es, ¿según x se aproxima más y más a c (pero x no es igual a c) se acerca f(x) más y más a un valor L? Si la respuesta es si, decimos que "f(x) tiende a L según x se aproxima a c", y se representa en forma simbólica de la forma:

La frase "x se aproxima a c" o "x tiende a c" significa que independientemente de lo próximo que esté x del valor c , existe siempre otro valor de x (distinto de c) en el dominio de f está aún más próximo a c .

Una función no puede tender a dos límites distintos a la vez. Esto es, si el límite de una función existe, es único.

Ejercicios de Aplicación:

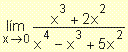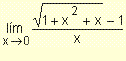Indeterminados:

En muchas ocasiones se presenta el cálculo de límites de cocientes, diferencias y productos de funciones en los que al reemplazar la variable por el valor al cual tiende se generan indeterminaciones del tipo 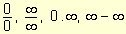. El resultado de estos límites no puede anticiparse y el mismo puede ser cero, ¥ , -¥ , un número finito diferente de cero, o bien puede no existir. Para resolverlos, se realizan procedimientos algebraicos adecuados que permitan salvar la indeterminación.

La indeterminación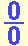 

Para salvar indeterminaciones de este tipo, es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador y/o el denominador, cancelando luego los factores comunes. En otras ocasiones, es posible crear un factor común multiplicando el numerador y el denominador por la expresión conjugada de la que se presenta en uno de ellos.

Ejemplo. Halle 
Al sustituir, resulta  y  lo que genera una indeterminación del tipo .

Sin embargo, como 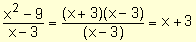 si x ¹ 3, resulta que la función  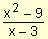coincide con la función (x + 3) salvo en x = 3.

Como interesa analizar el comportamiento de la función para valores de x próximos a 3 (por izquierda y por derecha), es posible determinar el comportamiento de 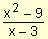 analizando el de la función (x + 3).

Por lo tanto puede decirse que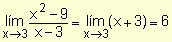 

   

Nota. Existe algo sospechoso en este ejemplo. Si el 3 no estaba en el dominio antes de simplificar, pero sí lo estaba después de simplificar, la función seguramente ha cambiado.

Al decir 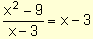 mentimos un poco. Lo que en realidad quisimos decir es que esas dos expresiones son iguales en donde están definidas. En realidad  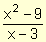y x + 3 son distintas. La diferencia entre ellas es que x = 3 no pertenece al dominio de  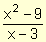pero sí al dominio de x + 3. Puesto que  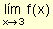ignora cualquier valor que f pueda tomar x = 3, eso no interesa. Desde el punto de vista del límite en 2 esas funciones sí son iguales.

   

Ejemplo. Calcule el valor de .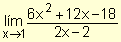

Al sustituir la variable por 1, tanto el numerador como el denominador se anulan y se genera la indeterminación 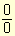. Se factorizan el numerador y el denominador y, para x ¹ 1, se simplifican los factores comunes:

   

Ejemplo. Halle el valor de .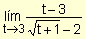

Reemplazando la variable por 3 se obtiene la indeterminación 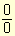. Para resolver este límite, se racionaliza el denominador multiplicando el numerador y el denominador por la expresión conjugada de la del denominador y resulta:

  

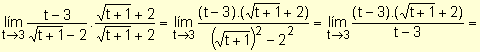
Ejemplo. Determine el límite .

Al sustituir, resulta 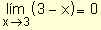 y  lo que genera una indeterminación del tipo .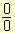

Si x ® 3, el denominador tiende a cero. Si x se aproxima a 3 por derecha o por izquierda, en cualquiera de los casos el denominador es positivo por estar elevado al cuadrado. Como el numerador negativo (-1), se concluye que el límite es -¥.

Ejemplos:

Ejercicios de Aplicación:

& Continuidad:

Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:

1. Que el punto x = a tenga imagen.

2. Que exista el límite de la función en el punto x = a.

3. Que la imagen del punto coincida con el límite de la función en el punto.

Ejemplo 

Estudiar la continuidad de 

 en x = 2

1. La función tiene imagen en x = 2.

f(2)= 4

2. La función tiene límite en x = 2 porque coinciden los límites laterales.

3. En x = 2 la imagen coincide con el límite

En la gráfica podemos comprobar que es continua.

Ejercicios de Aplicación: